发布人:繁体字网(www.fantiz5.com) 发布时间:2015-11-04 07:30:00
| 试题原文 |
|
| 解:A={x|x2﹣5x+4>0}={x|x<1或x>4}. ∵A∩B≠ 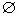 , , ∴方程x2﹣2ax+(a+2)=0有解,且至少有一解在区间(﹣∞,1)∪(4,+∞)内 直接求解情况比较多,考虑补集 设全集U={a|△≥0}=(﹣∞,﹣1]∪[2,+∞), P={a|方程x2﹣2ax+(a+2)=0的两根都在[1,4]内} 记f(x)=x2﹣2ax+(a+2),且f(x)=0的两根都在[1,4]内 ∴ 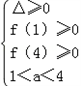 , ,∴ 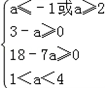 , ,∴ 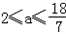 , ,∴ 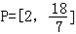 ∴实数a的取值范围为 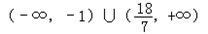 . . |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“(选做题)设集合A={x|x2﹣5x+4>0},B={x|x2﹣2ax+(a..”的主要目的是检查您对于考点“高中一元二次方程及其应用”相关知识的理解。有关该知识点的概要说明可查看:“高中一元二次方程及其应用”。