发布人:繁体字网(www.fantiz5.com) 发布时间:2015-05-23 07:30:00
| 试题原文 |
|
| 解:(1)成立; 证明:如图(2),∵∠PCM=∠PDM=90°, ∴点C、D在以PM为直径的圆上, ∴AC·AP=AM·MD,BD·BP=BM·BC, ∴AC·AP+BD·BP=AM·MD+BM·BC, 由已知,AM·MD+BM·BC=AB2, ∴AP·AC+BP·BD=AB2; (2)如图(3),过P作PM⊥AB, 交AB的延长线于M,连结AD、BC, 则C、M在以PB为直径的圆上,∴AP·AC=AB·AM,① D、M在以PA为直径的圆上,∴BP·BD=AB·BM,② 由图象可知:AB=AM-BM,③ 由①②③可得:AP·AC-BP·BD=AB·(AM-BM)=AB2。 | 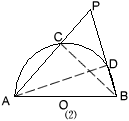 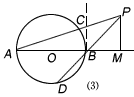 |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“阅读下面的材料:如图(1),在以AB为直径的半圆O内有一点P,AP、BP..”的主要目的是检查您对于考点“初中直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)”相关知识的理解。有关该知识点的概要说明可查看:“初中直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)”。