发布人:繁体字网(www.fantiz5.com) 发布时间:2016-02-01 07:30:00
| 试题原文 |
|
解:(Ⅰ)∵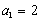 , ,∴ 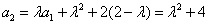 , ,同理,可得 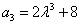 , ,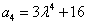 , ,猜想 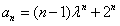 。 。(Ⅱ)假设数列 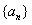 是等比数列,则 是等比数列,则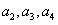 也成等比数列, 也成等比数列,∴ 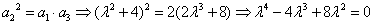 , ,∵ 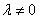 , ,∴ 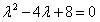 , ,即 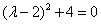 ,但 ,但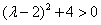 ,矛盾, ,矛盾, (Ⅲ)∵ 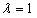 , ,∴ 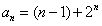 , ,∴ 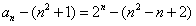 , ,∵当n=1,2,3时, 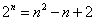 , ,∴ 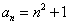 , ,当 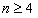 时,猜想 时,猜想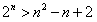 , ,证明如下:当n=4时,显然 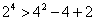 , ,假设 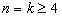 时,猜想成立,即 时,猜想成立,即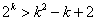 , ,则当n=k+1时, 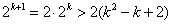 , ,∵ 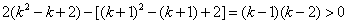 , ,∴ 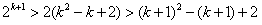 , ,∴当 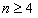 时,猜想 时,猜想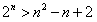 成立, 成立,∴当 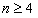 时, 时,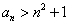 。 。 |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“在数列中,。(Ⅰ)求,并猜想数列的通项公式(不必证明);(Ⅱ)证明:当..”的主要目的是检查您对于考点“高中数学归纳法证明不等式”相关知识的理解。有关该知识点的概要说明可查看:“高中数学归纳法证明不等式”。