发布人:繁体字网(www.fantiz5.com) 发布时间:2015-12-05 07:30:00
| 试题原文 |
|
| 解:(1)由f(e)=2,代入f(x)=-ax+b+axlnx,得b=2; (2)由(1)可得f(x)=-ax+2+axlnx,函数f(x)的定义域为(0,+∞),从而f′(x)=alnx, ∵a≠0,故 ①当a>0时,由f′(x)>0得x>1, 由f′(x)<0得0<x<1; ②当a<0时,由f′(x)>0得0<x<1,由f′(x)<0得x>1; 综上,当a>0时,函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1); 当a<0时,函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞); (3)当a=1时,f(x)=-x+2+xlnx,f′(x)=lnx, 由(2)可得,当x∈( 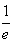 ,e),f(x),f′(x)变化情况如下表: ,e),f(x),f′(x)变化情况如下表: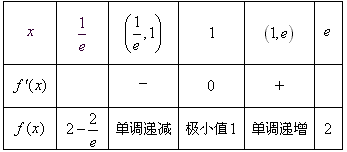 因为  所以y=f(x)在  上的值域为[1,2], 上的值域为[1,2],据此可得,若  则对每一个 则对每一个 直线 直线 与曲线 与曲线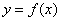  都有公共点;并且对每一个 都有公共点;并且对每一个 ,直线 ,直线 与曲线 与曲线  都没有公共点 都没有公共点综上,当  时,存在最小的实数 时,存在最小的实数 ,最大的实数 ,最大的实数 ,使得对每一个 ,使得对每一个 ,直线 ,直线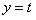 与曲线 与曲线 ( ( )都有公共点。 )都有公共点。 |
经过对同学们试题原文答题和答案批改分析后,可以看出该题目“已知a,b为常数,且a≠0,函数f(x)=-ax+b+axlnx,f(e)=2(e=2.718..”的主要目的是检查您对于考点“高中函数的单调性与导数的关系”相关知识的理解。有关该知识点的概要说明可查看:“高中函数的单调性与导数的关系”。